My senior year of high school, I was preparing for probably the hardest exam I’d ever have to take: my Anatomy and Physiology final exam. In order to make an A in the class, I had to make >92 on the exam. Our teacher gave us a pool of 500 questions; of those 500 questions, she would pick 100 to make up our exam. So, I set to work on memorizing the answers to those questions backwards and forwards.
Instead of using note cards (writing the question on the front and the answer on the back), I spent just as much work (maybe less) in writing a small PHP script that would import a list of ‘note cards’, prompt me with a random side (front or back) of a random card, hesitate (allow me to think of the answer), give me the answer upon my request, and allow me to mark whether or not I got it correct. At the end of this process (2 prompts (one for each side) * the # of cards = a long ass time), it gives me a list of the ‘note cards’ that I got wrong so that I can re-study them and re-test on them until I’ve mastered the material.
Keep in mind that this software was written while I was SUPPOSED to be studying, so I just hacked something together that would do the trick.
I have a nasty habit of forgetting code that I’ve written long ago, and I haven’t looked at this source for over a year, so I’m surprised at what I’ve found. Apparently, I had the intention of releasing this script in the future by the name of “Study Hard Software” (a working title, I’m sure); in fact, I’ve already licensed it to the GPL and commented it pretty heavily.
<?php
/*
Copyright (C) 2006 Michael Altfield
This file is part of Study Hard Software.
Study Hard Software is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
*/
/*
Import the crib sheet
The crib sheet is a file containing the questions and answers that Study Hard Software will pull in and display (ask) to the user. The format of the crib sheet is as follows:
question:answer
question:answer
...that is, each question and answer seperated by a colon (:), and each
individual question&answer combination is seperated by a newline.
Because the functioning of this application places
the formentioned question into the questions js array (q[]) AND into the the answers js array (a[]), and
the formentioned answer into the answers js array (a[]) AND into the questions js array (q[]),
the string to the left of the colon on the crib sheet is not *necessarly* a "question" at all.
The benefit of this is that the SHS asks you jepordy-like questions where it gives you the answer
and you have to think of the question--for absolute preperation for that exam :).
The result of this, however, is that we cannot call the string to the left a "question"
and the string to the right an "answer", as they could be ambigious. In the future, and
througout this application, the string to the left of the colon will be called "left" and
the string to the right of the colon will be called "right".
Now, Import the crib sheet
*/
$crib=file_get_contents($_GET['id']);
$file=explode("n",$crib);
for ($i=0;$i<sizeof($file);$i++) {
$file[$i]=explode(":",$file[$i]);
}
$iSentinal=sizeof($file)*2;
$num=0;
for ($i=sizeof($file);$i
var q=new Array();
var a=new Array();
var r=new Array();
pos=0;
sa='';
rb=' ';
<?
$iSentinel=sizeof($file);
for ($i=0;$i
//question
q[]="";
//answer
a[]="";
//result
r[]=0;
function showAnswer() {
document.getElementById("a").innerHTML=a[pos];
document.getElementById("b").innerHTML=rb;
document.getElementById("button").focus();
}
function markCorrect() {
r[pos]=1;
nextQ();
}
function markIncorrect() {
r[pos]=0;
nextQ();
}
function nextQ() {
if (pos<) {
pos++;
document.getElementById("b").innerHTML=sa;
document.getElementById("a").innerHTML=' ';
document.getElementById("q").innerHTML='Question #'+(pos+1)+"<br />"+q[pos];
document.getElementById("button").focus();
} else {
document.getElementById("b").innerHTML='';
document.getElementById("a").innerHTML='';
document.getElementById("q").innerHTML="Questions You Marked Incorrect:nn";
for (i=0;i<r.length;i++) {
if (r[i]==0) {
document.write("Question #"+(i+1)+": "+q[i]+"<br /> Answer: "+a[i]+"<br /><br />");
}
}
for (i=0;i<r.length;i++) {
if (r[i]==0) {
document.write(q[i]+":"+a[i]+"<br />");
}
}
}
}
<div>Question #1<br /></div>
<br /><br />
<div> </div>
<div></div>
I think the comments explain the software well enough, so I’m not going to reiterate how it works. I will, however, explain where to go once you get the code.
The script imports the ‘note cards’ from a ‘crib sheet’. This text file is formated like so:
question1:answer1 question2:answer2
When executing the script, you have to specify which crib sheet you would like to test yourself against. This is done by assigning the file’s name (which, by the way, must be in the same directory as the script itself) to a GET variable named ‘id’. For example, if you had your script on your local server (localhost) and you wanted to test yourself on the collegeElements crib sheet, you would type the following into your web browser:
http://localhost/index.php?id=collegeElements
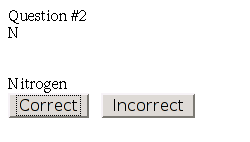
Here’s a sample execution of studying my elements.
Note how the Question #1 gives you the Element Name and asks for the Element’s Symbol.
Conversely, Question #2 gives you the Element’s Symbol and asks for the Element Name.
My crib sheet only has 50 lines (for 50 elements), yet “Study Hard Software” (that name is so lame) asked me 100 questions (2 for each note card–one backwards and one forwards).
After I’ve finished this study session (by going through the 100th question), I’m automatically prompted with all of the questions that I’ve answered incorrectly.
Note that this gives you both a human-readable list of the incorrectly answered questions AS WELL AS the crib sheet format. Personally, I like to re-study with the human-readable format, then I create another crib sheet (collegeElements2, perhaps) by copy & paste-ing the bottom half of this page.
Just for kicks, here’s that collegeElements crib sheet I used during the above sample execution
H:Hydrogen He:Helium Li:Lithium Be:Beryllium B:Boron C:Carbon N:Nitrogen O:Oxygen F:Fluorine Ne:Neon Na:Sodium Mg:Magnesium Al:Aluminum Si:Silicon P:Phosophorus S:Sulfur Cl:Chlorine Ar:Argon K:Potassium Ca:Calcium Sc:Scandium Ti:Titanium V:Vanadium Cr:Chromium Mn:Manganese Fe:Iron Co:Cobalt Ni:Nickel Cu:Copper Zn:Zinc Ga:Gallium Ge:Germanium As:Arsenic Se:Salenium Br:Bromine Pd:Palladium Ag:Silver Cd:Cadmium Sn:Tin I:Iodine Xe:Xenon Cs:Cesium Ba:Barium Pt:Platinum Au:Gold Hg:Mercury Pb:Lead Rn:Radon Ra:Radium U:Uranium
…also, there’s some bug in the code that causes a few ‘undefined’ questions to pop up after the last real question (probably just iterated one too many times). In any case, I just answer ‘correct’ to these, and it doesn’t affect the execution. I really don’t have enough time to fix it–nor do I care enough to do so.
Now that I’ve successfully procrastinated beyond my own capacity, I must write a crib sheet for my History exam tomorrow :-/
Related Posts
Hi, I’m Michael Altfield. I write articles about opsec, privacy, and devops ➡














Leave a Reply